how to find the altitude of a triangle
HOW TO FIND THE ALTITUDE OF A TRIANGLE WITH COORDINATES
About "How to find the altitude of a triangle with coordinates"
How to find the altitude of a triangle with coordinates :
Here we are going to see how to find slope of altitude of a triangle.
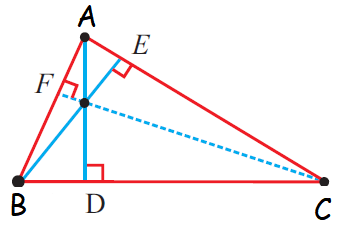
In the above triangle the line AD is perpendicular to the side BC, the line BE is perpendicular to the side AC and the side CF is perpendicular to the side AB.
The sides AD, BE and CF are known as altitudes of the triangle.
Slopes of altitude
Since the sides BC and AD are perpendicular to each other, the product of their slopes will be equal to -1
Slope of AD = -1/Slope of BC
Slope of BE = -1/Slope of AC
Slope of CF = -1/Slope of AB
Let us look into some example problems based on the above concept.
Question 1 :
The vertices of a triangle ABC are A(1 , 2), B(-4 , 5) and C(0 , 1). Find the slopes of the altitudes of the triangle.
Solution :
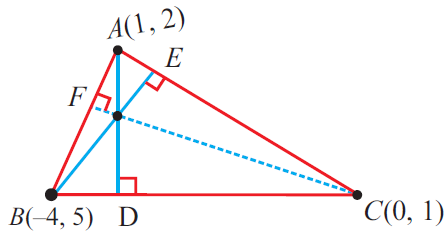
Slope of BC :
m = (y2- y1)/(x2- x1)
B (-4, 5) and C (0, 1)
m = (1 - 5)/(0-(-4))
= -4/(0 + 4)
= -4/4
= -1
Slope of AD = -1/Slope of BC
= -1/(-1)
= 1
Slope of AC :
m = (y2- y1)/(x2- x1)
A (1, 2) and C (0, 1)
m = (1 - 2)/(0-1)
= -1/(-1)
= 1
Slope of BE = -1/Slope of AC
= -1/1
= -1
Slope of AB :
m = (y2- y1)/(x2- x1)
A (1, 2) and B (-4, 5)
m = (5 - 2)/(-4 - 1)
= 3/(-5)
= -3/5
Slope of CF = -1/Slope of AB
= -1/(-3/5)
= 5/3
Hence the slopes of AD, BE and CF are 1, -1, and 5/3.
Related topics
- How to prove if the given points are collinear using slope
- Conditions for collinearity
- Conditions for collinearity of three points

After having gone through the stuff given on " How to find the altitude of a triangle with coordinates ", we hope that the students would have understood how to solve problems using unit rates.
Apart from the stuff given above, if you want to know more about " How to find the altitude of a triangle with coordinates ", please click here
Apart from the stuff given on " How to find slope of altitude of a triangle ", if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Algebra word problems
Word problems on trains
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on unit price
Word problems on unit rate
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Double facts word problems
Trigonometry word problems
Percentage word problems
Profit and loss word problems
Markup and markdown word problems
Decimal word problems
Word problems on fractions
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Time and work word problems
Word problems on sets and venn diagrams
Word problems on ages
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Profit and loss shortcuts
Percentage shortcuts
Times table shortcuts
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
how to find the altitude of a triangle
Source: https://www.onlinemath4all.com/how-to-find-the-altitude-of-a-triangle-with-coordinates.html
Posted by: malcolmcoging.blogspot.com

0 Response to "how to find the altitude of a triangle"
Post a Comment